Moth

In this simple reverse challenge we need to find the password for moth.

The binary

In Ghidra, we can have a quick look at the main function:

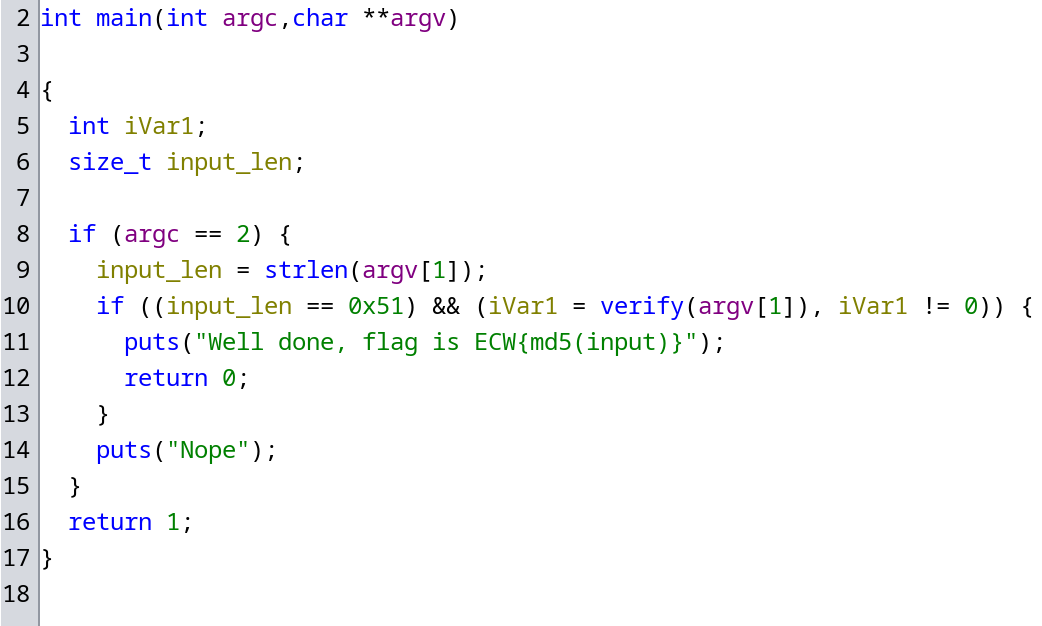
We need to find a 0x51 characters long password.

In verify, we seem to be performing 3 seperate checks in a 9 by 9 grid:

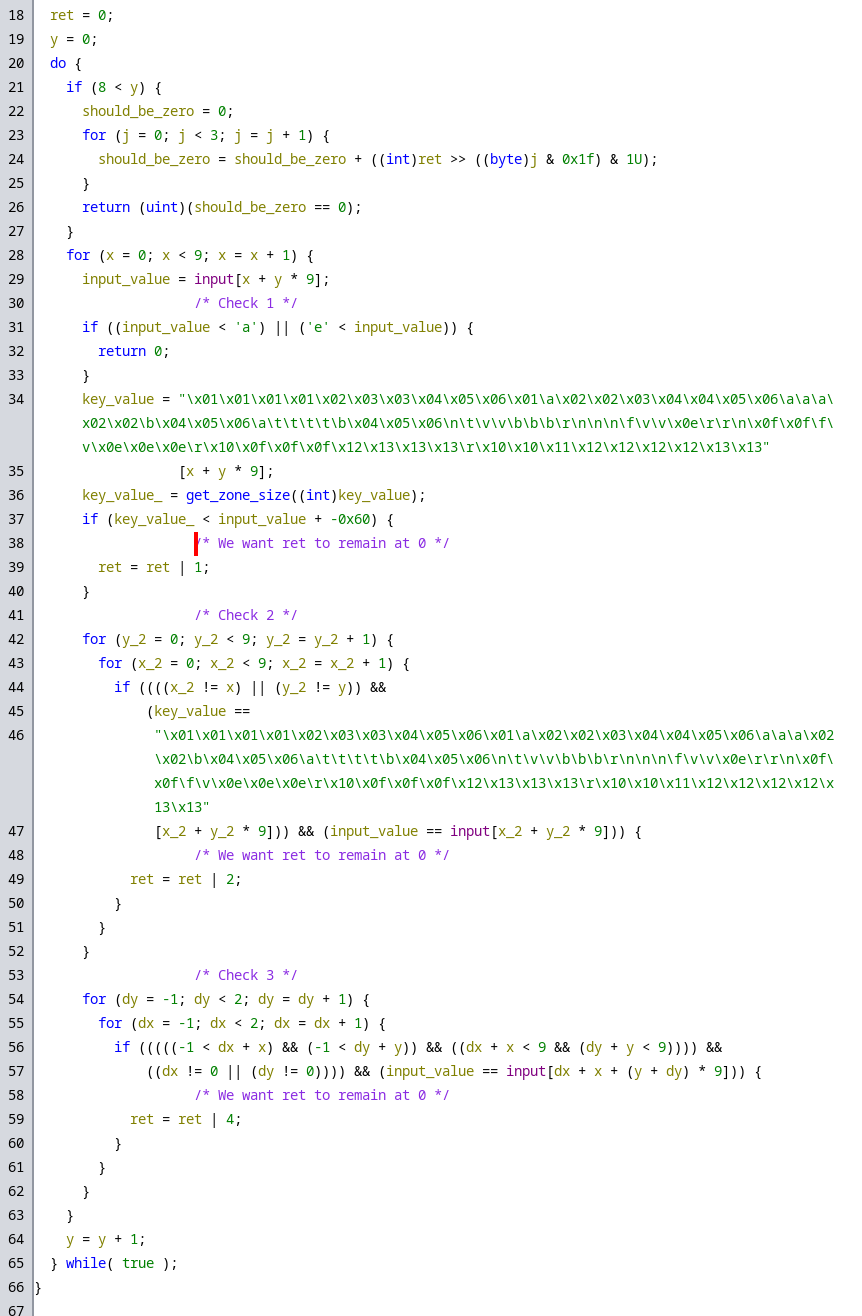
The first check makes sure that our value is be between 1 and 5 (‘a’ to ‘e’) and that it smaller than our zone size (We are calling a zone a group of characters in the key with the same value).

The second check makes sure that if the key has the same value at 2 coordinates then our password must have different values. In other words, in a given zone, each value needs to be distinct.

The last check makes sure that two adjacent cells (orthogonally or diagonally) have different values.

These checks looks a lot like sudoku checks…

The puzzle

If you are into sudokus (or an avid Cracking the cryptic fan) you can try and solve this puzzle by hand:

Here are the rules:

• Every zone has every digit from 1 to the size of the zone
• Orthogonal and diagonal cells cannot have the same value

TRADITIONAL SUDOKU RULES DO NOT APPLY

Wave function collapse

If you are too lazy to solve the above problem by hand you can always write a program to do so.

My preferred method for sudoku like problems is using the wave function collapse algorithm.

Here’s how the algorithm goes:

• Set the initial constraints on each cell
• While there remain undecided cells (a cell with more than one value)
  • Find the most constrained undecided cell
  • Chose a value in the available values for that cell
  • Propagate this change by modifying the constraints of every necessary cell
  • If a cell is over constrained -> backtrack

Here’s my python implementation that solves this problem

import copy

def reduce(grid: list[list[set[int]]], x: int, y: int, value: int):
    grid = copy.deepcopy(grid)
    color = g[y][x]

    # No same number in a given color
    for yy in range(9):
        for xx in range(9):
            if g[yy][xx] != color:
                continue
            if xx == x and yy == y:
                continue
            if value in grid[yy][xx]:
                grid[yy][xx].remove(value)

    # No same number around around
    for dy in [-1, 0, 1]:
        for dx in [-1, 0, 1]:
            if dy == 0 and dx == 0:
                continue
            if x + dx < 0 or x + dx >= 9:
                continue
            if y + dy < 0 or y + dy >= 9:
                continue
            if value in grid[y + dy][x + dx]:
                grid[y + dy][x + dx].remove(value)

    return grid

def verify(grid: list[list[set[int]]]):
    for y in range(9):
        for x in range(9):
            if len(grid[y][x]) == 0:
                raise ValueError("Empty cell")


def solve(grid: list[list[set[int]]], stack: list[tuple[int, int]], indentation=0):
    if len(stack) == 0:
        return grid

    stack.sort(key=lambda coords: len(grid[coords[1]][coords[0]]))

    x, y = stack.pop(0)

    values = [v for v in grid[y][x]]
    for v in values:
        try:
            grid[y][x] = set([v])
            grid2 = reduce(grid, x, y, v)
            verify(grid2)
            return solve(grid2, copy.deepcopy(stack), indentation=indentation+1)
        except ValueError as e:
            continue
    raise ValueError()

grid = [[set(range(1, g2[y][x] + 1)) for x in range(9)] for y in range(9)]
all = [(x, y) for x in range(9) for y in range(9)]
SOLUTION = solve(grid, all)
print(SOLUTION)
print(''.join([''.join([['a', 'b', 'c', 'd', 'e'][list(SOLUTION[y][x])[0] - 1] for x in range(9)]) for y in range(9)]))

Here is the solved grid:

[[{2}, {3}, {1}, {5}, {4}, {2}, {1}, {2}, {1}],
 [{1}, {4}, {2}, {3}, {1}, {3}, {4}, {3}, {4}],
 [{2}, {3}, {1}, {4}, {2}, {5}, {2}, {1}, {2}],
 [{4}, {5}, {2}, {5}, {3}, {1}, {3}, {5}, {3}],
 [{3}, {1}, {4}, {1}, {4}, {5}, {4}, {1}, {2}],
 [{4}, {2}, {5}, {2}, {3}, {2}, {3}, {5}, {4}],
 [{3}, {1}, {3}, {1}, {5}, {4}, {1}, {2}, {1}],
 [{2}, {5}, {2}, {4}, {2}, {3}, {5}, {4}, {3}],
 [{1}, {3}, {1}, {3}, {5}, {4}, {1}, {2}, {1}]]

Flag

Here is the password for the binary: bcaedbabaadbcacdcdbcadbebabdebecaceccadadedabdbebcbcedcacaedababebdbcedcacacedaba

When we run the binary with this password we get:

Well done, flag is ECW{md5(input)}

FLAG: ECW{8b39553c944cdce4ea4f9a692168093b}